الرياضيات وراء الأوكتاف

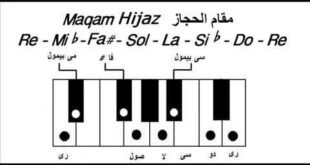
1. العلاقة الرياضية بين النغمات:
   في الموسيقى، يتم تقسيم الأوكتاف إلى 12 نصف نغمة متساوية. عندما تتحرك بين نغمتين متتاليتين (مثل “دو” إلى “دو#” أو “مي” إلى “فا”)، فإنك تتحرك بمقدار نصف نغمة. هذه التقسيمة تعتمد على مفهوم رياضي يسمى النسبة الأسية.
2. النسبة الأسية للأوكتاف:
   إذا كان لديك نغمة معينة بتردد ( f )، فإن النغمة التي تكون أعلى بمقدار نصف نغمة سيكون ترددها مضروباً في الجذر الثاني عشر للعدد 2 (( \sqrt[12]{2} )). وبالتالي، للوصول إلى نغمة أعلى بمقدار أوكتاف كامل، تحتاج إلى مضاعفة التردد الأصلي، وهذا يتم من خلال مضاعفة ( \sqrt[12]{2} ) لعدد 12 مرة، وهو ما يعيدك إلى تردد مضاعف (أي 2 * ( f )).
3. الصيغة الرياضية للأوكتاف:
   الصيغة الأساسية لتحديد تردد أي نغمة في أوكتاف معين هي:
   [
   f_n = f_0 \times (2^{(n/12)})
   ]
   حيث:

• ( f_n ) هو تردد النغمة التي نبحث عنها.
• ( f_0 ) هو تردد النغمة الأصلية.
• ( n ) هو عدد نصف النغمات بين النغمتين.

1. التطبيقات العملية:
   هذه المعرفة الرياضية مفيدة للموسيقيين عند ضبط الآلات الموسيقية، لأنها تتيح لهم تحديد الترددات الصحيحة لكل نغمة. كما تساهم في فهم كيفية تأثير تغيير الترددات على الصوت والإحساس الموسيقي، مما يساعد في التأليف الموسيقي وتطوير الألحان.
2. الأوكتاف كعنصر توازن في الموسيقى:
   الأوكتاف يُعتبر قاعدة للتوازن الموسيقي، حيث يمكن استخدامه لتوسيع نطاق الأصوات التي يمكن أن تُعزف أو تُغنى. يُعتبر الأوكتاف أداة قوية في تأليف الموسيقى حيث يتيح للفنانين التنقل بين النغمات المختلفة بسلاسة دون فقدان الانسجام أو الجمالية.

ختامًا:

الأوكتاف ليس مجرد مفهوم موسيقي، بل هو نتيجة لقاعدة رياضية أساسية تلعب دوراً كبيراً في فهم الصوت والموسيقى. فهم الأوكتاف وكيفية حسابه يمنح الموسيقيين أداة قوية لإثراء موسيقاهم وإضافة العمق والتنوع للألحان.

هذا الاستخدام للرياضيات يعكس مدى ارتباط العلوم بالفنون، ويجعل تعلم الموسيقى تجربة أكثر شمولية وإبداعاً!